Comprendre les algorithmes de tri en 7 minutes

Les algorithmes de tri permettent la compréhension de notions fondamentales en informatique. Ça tombe aussi très souvent en entretien d’embauche ! Ça prend quelques minutes à comprendre et ça va vraiment te servir un jour ou l’autre.

Oui, ça va te servir

Tu n’utiliseras pas le contenu de cet article tous les jours dans un vrai boulot. Dans la vraie vie, les algorithmes de tri, en particulier ceux d’aujourd’hui, sont déjà implémentés dans les langages de haut niveau.

Mais un beau jour tu vas débarquer en entretien de façon nonchalante en te disant que tu sais tout. Et là, on va te demander d’implémenter un tri fusion. Tu vas te sentir seul à regarder l’écran et ne plus savoir quoi faire.

Ne pas savoir tout ça ne t’empêchera pas d’être un bon développeur. Par contre, ça pourrait t’empêcher l’entrée de nombreuses entreprises. Comme je disais dans l’article précédent, c’est pas moi qui fais les entretiens.

Ceci dit, c’est un excellent exercice de connaitre et implémenter ces algos. C’est jamais perdu de comprendre comment fonctionnent les choses que tu utilises tous les jours sans le savoir. Et les algos de tris utilisent des concepts qui te serviront pour d’autres algos !

Bon t’es convaincu ? Aujourd’hui on va pas parler des plus importants et on va se focaliser plus sur la logique qu’autre chose. Comme d’habitude, on commence par le plus simple.

Tri à bulles (bubble sort)

Le tri à bulles est de loin le plus simple de tous les algos de tri. D’ailleurs c’est pour ça qu’il est super lent et quasiment jamais utilisé. Mais c’est un classico. Si tu le connais pas, c’est pas normal.

La logique est simple:

• On passe sur chaque élément du tableau et on le compare à son voisin de droite.
• Si le voisin de droite est plus petit alors les deux éléments permutent, car l’élément le plus petit devrait être à gauche.
• On fait autant de passe que nécessaire jusqu’à que tout le tableau soit trié.

La condition d’arrêt étant le fait qu’aucune permutation n’ait été nécessaire dans une passe. Easy !

Pour que tu captes vraiment la logique, il faut qu’on regarde ça plus concrètement. La façon la plus simple de visualiser ce genre d’algo est une animation.

Aujourd’hui je ne vais pas te faire mes dessins maison, ou mes « oeuvres modernes » comme je les appelle. La raison est simple : les animations qu’on trouve sur les internet sont juste trop parfaites. Par exemple, celle-ci trouvera sur ce site de geek.

Comme image mentale que tu peux te faire de cet algorithme : les bulles d’une coupe de champagne. Cet algorithme pousse rapidement les plus gros chiffres à trier en fin de tableau, comme des bulles de champagnes qui remonte à la surface.

OK, super mes histoires de champagnes, comment on code ça ?

Javascript (NodeJS 12.14.0)

const unsortedArray = [2020, 1998, 2018, 1986, 2006]

const bubbleSort = array => {
  const arrayLength = array.length
  let isSwapped

  do {
    isSwapped = false

    for (let i = 0; i < arrayLength - 1; i++) {
      if (array[i] > array[i + 1]) {
        const tempLeftValue = array[i]
        array[i] = array[i + 1]
        array[i + 1] = tempLeftValue

        isSwapped = true
      }
    }
  } while (isSwapped)

  return array
}

console.log(bubbleSort(unsortedArray))
// [ 1986, 1998, 2006, 2018, 2020 ]

Comme tu peux l’imaginer, les performances de cet algorithmique sont vraiment pas bonnes. On est sur une tendance quadratique O(n²) dans le pire des cas. C’est parce qu’on fait une passe linéaire sur tout le tableau et une autre par élément.

Tri par insertion (Insertion sort)

Le tri par insertion fait également partie des algorithmes de tri les plus simples à comprendre et à utiliser. Et comme souvent, sa simplicité vient avec le prix d’une mauvaise performance sur de larges séquences de données. On est toujours sur un algorithme assez lent avec beaucoup de données, mais efficace sur peu.

La logique de cet algorithme est, je trouve, très intuitive.

• On passe sur chacun des éléments à trier et on l’insère directement à la place où il devrait être.
• Pour faire cette insertion, on va simplement comparer l’élément courant avec chaque élément déjà trié sur la gauche.

Pour mieux comprendre une belle visualisation animée absolument pompée sur cet antre à geek.

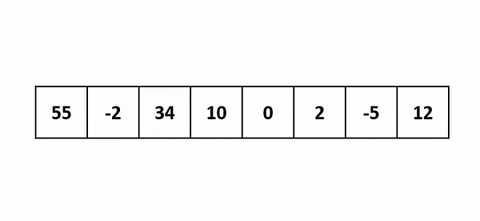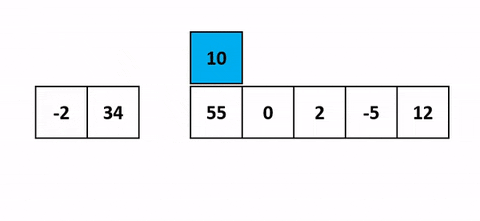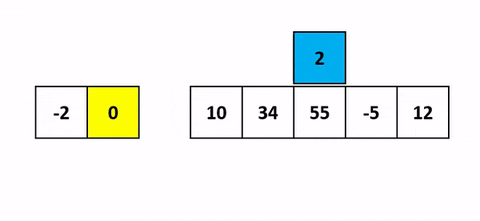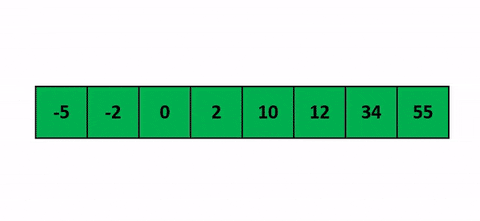
J’ai une belle image mentale pour celui-là. Quand tu joues aux cartes et que tu dois trier ta main en début de partie, tu fais comment ? Tu vas prendre chaque carte une à une et tu vas trier en les insérant au fur et à mesure sur la gauche. Cet algo c’est pareil.

Et du coup, comment on code tes mains ?

Python (3.6.9)

unsorted_array = [2018, 1998, 1986, 2020, 2006]

def insertion_sort(array_to_sort):
    for index in range(1, len(array_to_sort)):
        current_item = array_to_sort[index]
        current_left_index = index - 1

        while current_left_index >= 0 and array_to_sort[current_left_index] > current_item:
            array_to_sort[current_left_index + 1] = array_to_sort[current_left_index] 
            current_left_index -= 1

        array_to_sort[current_left_index + 1] = current_item

    return array_to_sort

print(insertion_sort(unsorted_array))
# [1986, 1998, 2006, 2018, 2020]

Malgré sa tendance quadratique O(n²) dans le pire des cas, le tri par insertion est considéré comme l’un des meilleurs algorithmes de tri pour de petites séquences de données !

D’ailleurs tiens changeons de famille. Comment on fait pour trier de grandes séquences de données ?

Tri fusion (merge sort)

Le tri fusion est un algorithme de la grande famille des algorithmes « diviser pour régner« . Il est légèrement plus complexe que les algorithmes précédents, mais son efficacité est redoutable ! En particulier sur de grandes séquences de données.

Cet algorithme de tri a une logique un peu plus complexe.

• On va commencer par diviser le tableau en deux éléments égaux.
• On va recommencer la même chose jusqu’à atteindre un seul élément par séparation.
• Ensuite, on va refusionner les éléments séparés de façon récursive en les triant à chaque niveau.

C’est en comparant et permutant les éléments niveau par niveau qu’on construit un nouveau tableau trié ! C’est toujours plus clair avec une belle visualisation.

L’image mentale que j’utilise pour m’en souvenir est les poupées russes. Le comportement de décomposition du tableau de façon récursive jusqu’à son plus petit élément est très similaire. Regardons comment on implémente ça.

Comme cet algo est un peu plus compliqué que les précédents, je t’ai mis des commentaires qui expliquent chaque étape du code. En regardant la visualisation au dessus plus les commentaires de la logique dans le code, ça devrait être plus clair si tu découvres tout ça.

C’est normal d’avoir un peu de mal à suivre la récursion ici, on en reparlera dans un prochain article.

Javascript (NodeJS 12.14.0)

const mergeSort = array => {
  // divide array until there's only one element
  // the recursive stop condition !
  if (array.length > 1) {
    // get the middle index of the current division
    const middleIndex = Math.floor(array.length / 2)
    // get left side
    const leftSide = array.slice(0, middleIndex)
    // get right side
    const rightSide = array.slice(middleIndex)

    // call recursively for the left part of the data
    mergeSort(leftSide)
    // call recursively for the right part of the data
    mergeSort(rightSide)

    // default setup of the indexes
    let leftIndex = 0, rightIndex = 0, globalIndex = 0

    // loop until we reach the end of the left or the right array
    // we can't compare if there is only one element
    while(leftIndex < leftSide.length && rightIndex < rightSide.length) {
      // actual sort comparaison is here
      // if the left element is smaller its should be first in the array
      // else the right element should be first
      // move indexes at each steps
      if (leftSide[leftIndex] < rightSide[rightIndex]) {
        array[globalIndex] = leftSide[leftIndex]
        leftIndex++
      } else {
        array[globalIndex] = rightSide[rightIndex]
        rightIndex++
      }
      globalIndex++
    }

    // making sure that any element was not left behind during the process
    while(leftIndex < leftSide.length) {
      array[globalIndex] = leftSide[leftIndex]
      leftIndex++
      globalIndex++
    }

    while(rightIndex < rightSide.length) {
      array[globalIndex] = rightSide[rightIndex]
      rightIndex++
      globalIndex++
    }
  }

  return array
}

console.log(mergeSort([2020, 1998, 2018, 1986, 2006]))
// [1986, 1998, 2006, 2018, 2020]

Cet algorithme étant un algorithme de la famille « diviser pour régner » (divide and conquer) on est sur une complexité linéarithmique O(n log n) dans le pire de cas ! Ça fait de cet algorithme de tri l’un des plus optimisés, et donc l’un des plus utilisés.

C’est le tri fusion, ou une variante, qui est fréquemment utilisé dans les fonctions de tri que tu utilises tous les jours. En Javascript, ça dépend du navigateur (et donc du moteur Javascript). Sur Firefox ça sera le tri fusion, sur Chrome pour un grand tableau ça sera le tri rapide. Tiens d’ailleurs, parlons-en du tri rapide.

Tri rapide (quick sort)

Le tri rapide (quicksort), ou tri pivot, fait aussi partie de la famille des algorithmes « diviser pour régner ». Lui aussi utilise donc de la récursivité et sa logique est un peu plus complexe. Comme le tri fusion, il est cependant grandement utilisé dans les langages modernes.

Son fonctionnement est centré autour du concept du pivot.

On va choisir un élément dans le tableau et on va décréter que cet élément est le pivot pour une itération sur le tableau. Y’a différente façon de choisir un pivot, on ne va pas rentrer là-dedans, aujourd’hui le pivot sera toujours le dernier élément du tableau.

Une fois qu’on a ce pivot, on va créer un sous tableau.

• Toutes les valeurs plus basses que ce pivot vont à gauche de ce sous-tableau.
• Le pivot au milieu de ce sous-tableau.
• Toutes les valeurs plus grandes que ce pivot vont à droite.

Et ensuite on va appeler de façon récursive le même algo sur ce sous-tableau ! Celui-là est relativement difficile à comprendre du premier coup. Déjà il te faut un dessin pour visualiser cette affaire.

Pour cet algo j’utilise la même image mentale que le précédent. On retrouve cette idée de poupée russes dans le fonctionnement où on va résoudre un problème de plus en plus petit avant d’avoir un tableau trié. Y’a un juste un pivot au milieu.

Pour l’implémentation, je t’ai également rajouté des commentaires explicatifs à chaque étape pour que ça soit plus clair !

Python (3.6.9)

def quick_sort(array_to_sort):
    # if there is no smaller or bigger values we have nothing to sort anymore
    # array is sorted !
    # this is the recursive stop condition
    if not array_to_sort:
        return []
    else:
        # if we have value to sort we choose a pivot
        # here we just getting the last element of the array
        pivot = array_to_sort[-1]

        # we go through the current array and build an array 
        # of smaller values of the pivot
        array_of_smaller_values = [value for value in array_to_sort if value < pivot]

        # we go through the current array (minus the pivot) and build an array
        # of bigger values of the pivot
        array_of_bigger_values = [value for value in array_to_sort[:-1] if value >= pivot]

        # we return the current iteration with a new array
        # smaller values at the beggining, pivot in the middle, bigger values in the end
        return quick_sort(array_of_smaller_values) + [pivot] + quick_sort(array_of_bigger_values)

print(quick_sort([2018, 1998, 1986, 2020, 2006]))
# [1986, 1998, 2006, 2018, 2020]

La complexité moyenne du tri rapide est optimale avec une complexité linéarithmique O(n log n). Mais dans le pire des cas, le tri rapide a une complexité quadratique O(n²). Il est quand même énormément utilisé, car ce pire des cas est très peu probable. Il peut même être complètement évité avec la variation introsort du quicksort !

Épilogue

Il y a d’autres algorithmes de tri à connaitre. Mais ça fait déjà beaucoup pour une première introduction. Comme d’habitude y’a pas de secret, il faut que tu les implémentes un peu toi-même pour vraiment les comprendre et être confiant le jour de l’entretien. C’est vraiment pas si complexe que ça et en plus ça fait bosser l’algorithmie !